傅立叶变换:揭秘经济周期的神秘面纱
一、破解经济周期的密码
“经济周期,一直以来对我来说都是个谜。我曾在夜晚的闲暇时刻,独自坐在桌前,手握着一杯热咖啡,眼前摊开的是一堆无从理解的经济数据。我知道,这些数据背后隐藏着一个个周期性的秘密,它们像是一种神秘的密码,等待着我去破解。但是,我却不知道该如何下手。”
这是我,一位经济学家的困境。对于我们这样的专家来说,经济周期(Economic Cycles)的研究是我们工作中的一个重要部分。经济周期是经济活动中反复出现的上升和下降的波动。为了更好地理解和预测这些波动,我们需要找到一种方法,可以将这些复杂的数据分解为更易于理解的周期性成分。这就是傅立叶变换(Fourier Transform)发挥作用的地方。
二、傅立叶变换:一个强大的工具
傅立叶变换是一种在数学、物理和工程等领域广泛应用的数学技术,它的名字来源于18世纪的法国数学家傅立叶。在经济学中,傅立叶变换可以帮助我们分析经济数据的周期性。
想象一下,你在一片湖面上抛出一块石头,石头落水的地方会产生一圈圈的水波纹。这些水波纹的传播,就好像经济数据中的周期性波动。傅立叶变换,就像是一种超级显微镜,它可以帮助我们看清这些水波纹的细节,找出每一个波动的频率和强度。
三、实操:揭秘经济周期的神秘面纱
在实际操作中,我们首先需要收集一段时间内的经济数据。这些数据可以是国内生产总值(GDP)、物价指数、股票市场指数等。
接着,我们对这些数据进行傅立叶变换,得到它们的频谱。频谱上的每一个点代表了一个特定频率下的强度,这可以被理解为在该频率下的周期性成分的强度。
然后,我们就可以分析这个频谱,找出数据中的主要周期成分。如果一个特定频率下的强度特别高,那就意味着数据在该频率下有一个强周期性。通过计算该频率对应的周期,我们就可以找到经济数据的经济周期。
下面,我将以模拟的数据为例,详细展示这个过程。
四、模拟实验:解析经济周期
我创建了一些模拟的经济数据,这些数据包含两个主要的周期成分,一个周期为50,另一个周期为100,并且添加了一些随机噪声。
对这些数据进行傅立叶变换后,我得到了它们的频谱,如下图所示。在“原始信号”图中,我们可以看到信号随时间的变化。在“频谱”图中,我们可以看到信号在各个频率下的强度。
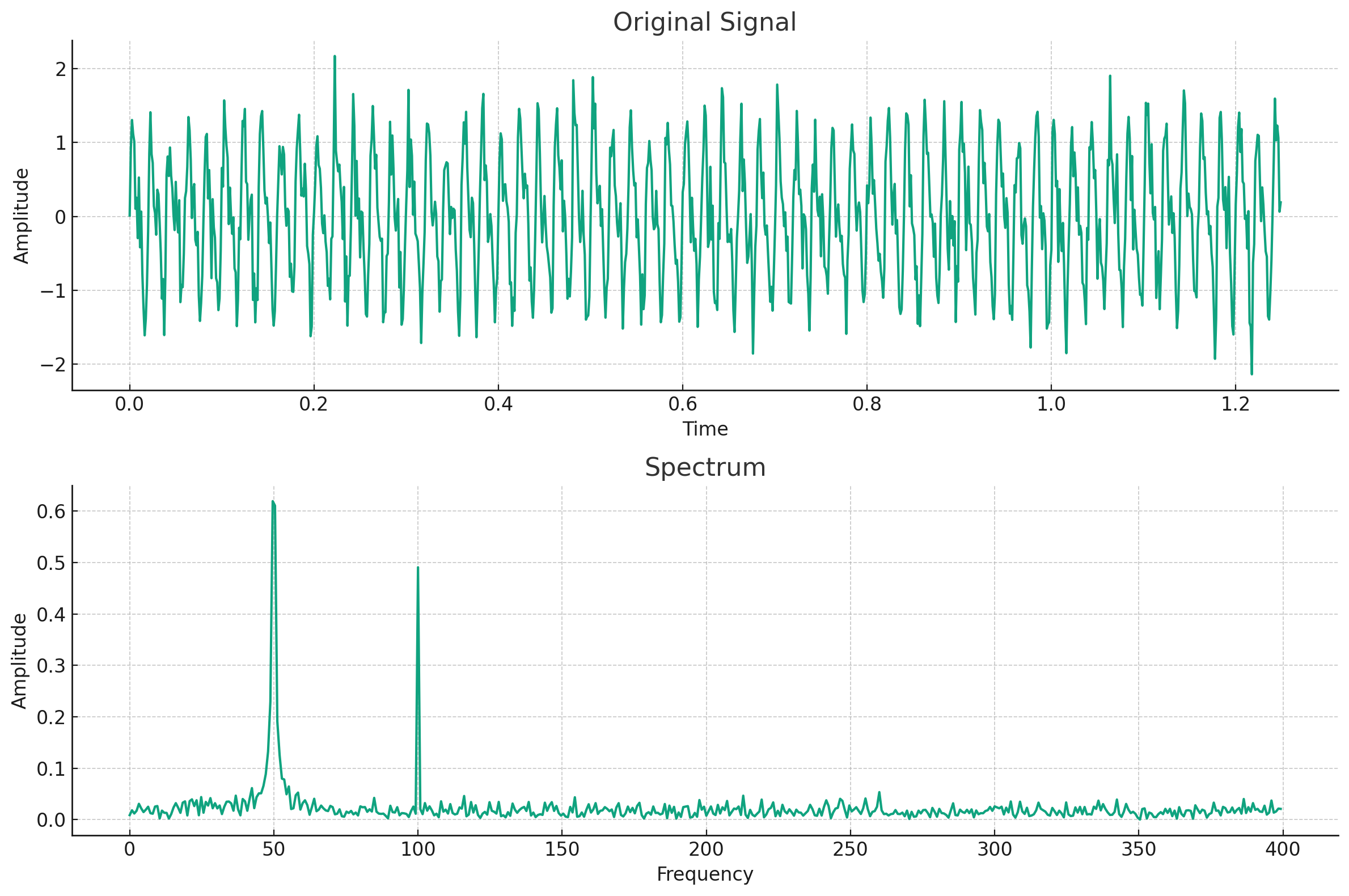
在频谱图中,我发现在频率为50和100处,强度显著高于其他地方,这表明信号在这两个频率下有强烈的周期性。通过这个分析,我找到了模拟经济数据中的主要周期成分。
五、反思:傅立叶变换的局限性
然而,正如每一枚硬币都有两面,傅立叶变换虽然强大,但它也有一些局限性。例如,它假设数据是平稳的,这在很多实际情况下并不成立。此外,傅立叶变换只能分析线性的周期性,对于非线性的周期性,傅立叶变换可能就无能为力了。
六、探索:未来的可能性
傅立叶变换,就像是一扇窗,让我们看到了经济周期的神秘面纱。然而,这扇窗还远远不够大,还有许多我们尚未看清的秘密。对于这些更深层次的秘密,我们需要更强大的工具,比如小波变换(Wavelet Transform)。与傅立叶变换相比,小波变换可以分析非线性的和非平稳的数据,因此,它在处理实际的经济数据时可能更有优势。
在这个旅程的最后,我想说,经济周期的研究就像是攀登一座高山。我们可能会遇到困难,可能会迷失方向,但只要我们不放弃,总会找到通往山顶的道路。而傅立叶变换,就是我们手中的一把钥匙,它能打开通
往理解的大门。让我们一起,揭秘经济周期的神秘面纱吧。