第三大脑

智能共生——万物互联，裂隙有光。

首页 归档 标签 关于 友链 转录

使用确定性有限自动机匹配10进制的倍数

2023-07-23 9 min read

在我们的数字世界中，计算机科学家常常面临一个看似平淡，却实际涉及复杂数学理论的问题：如何判断一个数是特定数的倍数？这可能看似是一个简单的问题，但其答案却需要我们走进计算机科学中最美的理论之一——自动机理论。在这里，我将尽力让你理解其中的奥秘，并通过一个实例，演示如何使用确定性有限自动机（DFA）来解决这个问题。

建立DFA的基本原理

一种有效的方式是使用一个具有n个状态的DFA，每个状态对应着0到n-1之间的一个余数。起始状态是0，因为在我们开始时，我们的数没有任何值，所以对任何数取余都是0。接受状态也是0，因为只有当一个数是n的倍数时，它模n的余数才是0。

让我们来构造DFA的转移函数。在任意给定的状态k，当读入数字m时，我们需要决定下一个状态。下一个状态r可以用这个公式计算：r = (10k + m) mod n。这个状态的转变，就像是在按照特定的舞步，在自动机的状态空间中跳舞。

实例：判断一个数是否是3的倍数

例如，当我们要判断一个数是否是3的倍数，我们会有三个状态：0, 1, 2。这三个状态分别对应于一个数模3的余数。这个DFA的构造如同我们在一个三角形的三个顶点跳舞。每一个数字，如同音乐中的每一拍，会引导我们向下一个顶点移动。

假设当前状态是1，即当前的数模3的余数是1，我们读取的下一个数字是5，那么下一个状态就是(10 * 1 + 5) mod 3 = 2。就像是在舞曲的引导下，我们从一个顶点跳到了另一个顶点。

在这个DFA中，我们可以创建如下的转移函数：

  • 0 --0--> 0
  • 0 --1--> 1
  • 0 --2--> 2
  • 1 --0--> 0
  • 1 --1--> 1
  • 1 --2--> 2
  • 2 --0--> 0
  • 2 --1--> 1
  • 2 --2--> 2

每个状态都有与0-9对应的10个转移，就像每个舞步都有10种可能的变化。

从抽象到具体：DFA的性质

这就是我们的自动机，它仿佛一个迷宫，用来指引我们判断一个数是否是n的倍数。然而，这个迷宫并非仅仅是一个解题工具，它更像是一种对数字世界的思考方式，一种把抽象的数学问题具象化的方式。

实际上，这个DFA就是在模拟我们对一个数进行除法的过程。每次读取一个数字，就相当于将当前的余数乘以10然后加上这个数字，然后求余。就像我们在纸上进行长除法一样。因此，这个DFA可以保证对于任何输入的数字，最后都会停在正确的余数的状态上。

我想让你记住的是，计算机科学并不只是关于编程和算法，它也是关于如何看待世界，如何用数学的语言描述我们的问题，并找到美丽的解决方案。我们使用的这个自动机，就是这样一种美丽的解决方案。它是对数字的一种全新的理解方式，是一种数学和艺术的结合，是理性与感性的交汇。

如何从给定的 DFA 得到相应的正则表达式的步骤。

在这个过程中，我将使用一种被称为“状态消除法”的算法。基本的想法是逐个消除非初始和非终态的状态，每次消除一个状态都需要更新正则表达式。在每个步骤中，所有进入被消除状态的边和所有从被消除状态出去的边会被替换为新的边，这些新的边代表了所有通过被消除状态可以实现的状态转换。

让我们看看如何在给定的 DFA 上应用这个算法：

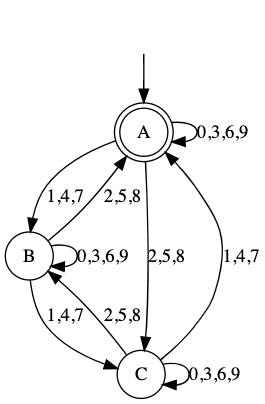
初始的 DFA（用正则表达式表示边）如下：

start -> A
A -> A [label="0,3,6,9"];
A -> B [label="1,4,7"];
A -> C [label="2,5,8"];
B -> B [label="0,3,6,9"];
B -> A [label="2,5,8"];
B -> C [label="1,4,7"];
C -> C [label="0,3,6,9"];
C -> A [label="1,4,7"];
C -> B [label="2,5,8"];

第一步，我们消除状态 B：

  1. A 到 C 的新边是 “A 到 B 的边，跟着 B 的自循环任意次（也可能为零次），然后是 B 到 C 的边”。所以，新的边是 A 到 C，标签是 (1,4,7)(0,3,6,9)*2,5,8。
  2. A 到 A 的新边是 “A 到 B 的边，跟着 B 的自循环任意次（也可能为零次），然后是 B 到 A 的边”。所以，新的边是 A 到 A，标签是 (1,4,7)(0,3,6,9)*2,5,8。
  3. 同理，C 到 A 和 C 到 C 的新边分别是 2,5,8(0,3,6,9)*2,5,8 和 2,5,8(0,3,6,9)*1,4,7。

所以，我们现在的 DFA（用正则表达式表示边）是：

start -> A
A -> A [label="0,3,6,9|(1,4,7)(0,3,6,9)*2,5,8"];
A -> C [label="2,5,8|(1,4,7)(0,3,6,9)*1,4,7"];
C -> C [label="0,3,6,9|2,5,8(0,3,6,9)*1,4,7"];
C -> A [label="1,4,7|2,5,8(0,3,6,9)*2,5,8"];

第二步，我们消除状态 C：

  1. A 到 A 的新边是 “A 到 C 的边，跟着 C 的自循环任意次（也可能为零次），然后是 C 到 A 的边”。所以，新的边是 A 到 A，标签是 0,3,6,9|(1,4,7)(0,3,6,9)*2,5,8|(2,5,8|(1,4,7)(0,3,6,9)*1,4,7)(0,3,6,9|2,5,8(0,3,6,9)*1,4,7)*(1,4,7|2,5,8(0,3,6,9)*2,5,8)。

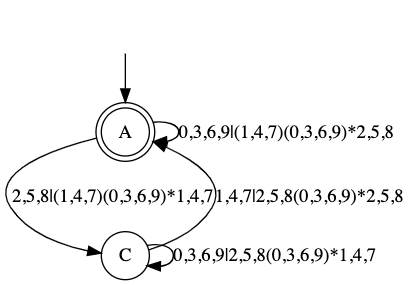
所以，最终的 DFA（用正则表达式表示边）是：

start -> A
A -> A [label="0,3,6,9|(1,4,7)(0,3,6,9)*2,5,8|(2,5,8|(1,4,7)(0,3,6,9)*1,4,7)(0,3,6,9|2,5,8(0,3,6,9)*1,4,7)*(1,4,7|2,5,8(0,3,6,9)*2,5,8)"];

其中，| 表示正则表达式中的 “或” 操作，* 表示任意次（包括零次）的重复。这就是最终的正则表达式，描述了从初始状态 A 到终态 A 的所有可能路径。

需要注意的是，由于这个方法是用正则表达式直接描述状态转移，所以得到的正则表达式可能比实际需要的正则表达式要复杂。在实际使用中，可能需要通过简化正则表达式来得到更简洁、更易理解的结果。

digraph G {

node [shape=circle]
A [shape=doublecircle];
start [shape=plaintext, label=""]

start -> A
A -> B [label="1,4,7"];
B -> C [label="1,4,7"];
C -> A [label="1,4,7"];
A -> A [label="0,3,6,9"];
B -> B [label="0,3,6,9"];
C -> C [label="0,3,6,9"];
A -> C [label="2,5,8"];
C -> B [label="2,5,8"];
B -> A [label="2,5,8"];
}

Graphviz Online

Regex Golf

https://chat.openai.com/share/5a109fed-1e82-4ce0-a46e-59470cc6271a

(99 封私信) 正则表达式如何匹配 3 的倍数？ - 知乎

Powered by Gridea RSS